Histoire des mathématiques - Définition
| Article de la série Histoire des sciences |
| Chronologie |
|---|
| Frise chronologique |
| Chronologie de l'astronomie |
| Sciences de l'Antiquité |
| Sciences au Moyen Âge |
| XVe s. - XVIe s. |
| XVIIe s. - XVIIIe s. |
| XIXe s. - XXe s. |
| Thématiques |
| Sciences grecques |
| Sciences chinoises |
| Sciences indiennes |
| Sciences islamiques |
| Histoire... |
| de l'astronomie |
| des mathématiques |
| de la biologie |
| de la médecine |
| de la physique |
| de l'électricité |
| de la zoologie & botanique |
| de l'écologie |
| des sciences du langage |
| Voir aussi |
| Science |
| Histoire des sciences (discipline) |
| Philosophie des sciences |
| Épistémologie |
| Sociologie des sciences |
| Méta |
| Projet |
L’histoire des mathématiques s'étend sur plusieurs millénaires et dans de nombreuses régions du globe allant de la Chine à l'Amérique centrale. Dans la mesure où historiquement la recherche en mathématiques s'est concentrée dans divers endroits du globe, dans le présent article nous proposons une approche par îlots géographiques.
Préhistoire
Avant l'apparition de l'écriture, des dessins reflètent des premières connaissances mathématiques. Dans une caverne en Afrique du Sud, des paléontologues ont retrouvé des peintures ocres ornées de figures géométriques, datant de 70 000 avant notre ère[réf. nécessaire]. Des artéfacts préhistoriques ont été retrouvés, datant d'entre 37 000 et de 20 000 avant notre ère attestent des premières tentatives de mesurer le temps[1]. Les concepts de un, deux et beaucoup étaient connus.
L'os d'Ishango datant de 20 000 ans avant notre ère est généralement cité pour être la première preuve de la connaissance des premiers nombres premiers et de la multiplication[réf. nécessaire], mais cette interprétation reste sujette à discussions[réf. nécessaire]. Il est dit que les mégalithes en Égypte au Ve millénaire avant notre ère ou en Angleterre au IIIe millénaire incorporeraient des idées géométriques comme les cercles, les ellipses et les triplets pythagoriciens[réf. nécessaire]. En 2 600 avant notre ère, les constructions égyptiennes attestent d'une connaissance précise et réfléchie de la géométrie[réf. nécessaire].
L'ethnomathématiques est un domaine de recherche à la frontière de l'anthropologie, de l'ethnologie et des mathématiques qui vise entre autres à comprendre l'essor des mathématiques dans les premières civilisations à partir des objets, instruments, peintures, et autres documents retrouvés.
De Sumer à Babylone
On situe en général les débuts de l'écriture à Sumer, dans le bassin du Tigre et de l'Euphrate ou Mésopotamie. Cette écriture, dite cunéiforme, naît du besoin d'organiser l'irrigation [2] et le commerce. Conjointement à la naissance de l'écriture naissent les premières mathématiques utilitaires (économie, calculs de surface). Le premier système numérique positionnel apparaît : le système sexagésimal. Pendant près de deux mille ans, les mathématiques vont se développer dans la région de Sumer, Akkad puis Babylone. Les tablettes datant de cette période sont constituées de tables numériques et de modes d'emploi. C'est ainsi qu'à Nippur (à une centaine de km de Bagdad), ont été découvertes au XIXe siècle des tablettes scolaires datant de l'époque paléo-Babylonienne (2000 av. J.-C.)[3]. On sait donc qu'ils connaissaient les quatre opérations mais se sont lancés dans des calculs plus complexes avec une très grande précision, comme des algorithmes d'extraction de racines carrées[4], racines cubiques, la résolution d'équations du second degré. Comme ils faisaient les divisions par multiplication par l'inverse, les tables d'inverse jouaient un grand rôle. On en a retrouvé avec des inverses pour des nombres à six chiffres sexagésimaux, ce qui indique une très grande précision [5]. On a également retrouvé des tablettes sur lesquelles figurent la liste des carrés d'entier, la liste des cubes et la liste des triplets pythagoriciens[6] montrant qu'ils connaissaient la propriété des triangles rectangles plus de 1 000 ans avant Pythagore. Des tablettes ont aussi été retrouvées décrivant des algorithmes pour résoudre des problèmes complexes [7].
Ils étaient capables d'utiliser des interpolations linéaires pour les calculs des valeurs intermédiaires ne figurant pas dans leurs tableaux. La période la plus riche concernant ces mathématiques est la période de Hammurabi (XVIIIe siècle av. J.-C.). Vers 1000 av. J.-C., on observe un développement du calcul vers l'astronomie mathématique[8].
Égypte
Les meilleures sources sur les connaissances mathématiques en Égypte antique sont le Papyrus Rhind (seconde période intermédiaire, XXe siècle avant J.-C.) qui développe de nombreux problèmes de géométrie, et le Papyrus de Moscou (1850 avant J.-C.) et le rouleau de cuir. À ces documents s'ajoutent trois autres papyrus et deux tablettes de bois ; le manque de documents ne permet pas d'attester ces connaissances[9]. Les Égyptiens ont utilisé les mathématiques principalement pour le calcul des salaires, la gestion des récoltes, les calculs de surface et de volume et dans leurs travaux d'irrigation et de construction (voir Sciences Égyptiennes). Ils utilisaient un système d'écriture des nombres additionnel (numération égyptienne). Ils connaissaient les quatre opérations, étaient familiers du calcul fractionnaire (basé uniquement sur les inverses d'entiers naturels) et étaient capables de résoudre des équations du premier degré par la méthode de la fausse position. Ils utilisaient une approximation fractionnaire de π[10]. Les équations ne sont pas écrites, mais elles sous-tendent les explications données.
Chine
La source principale la plus ancienne de nos connaissances sur les mathématiques chinoises provient du manuscrit de Zhoubi Suanjing ou Les neuf chapitres sur l'art mathématique, qui regroupe des connaissances datant de l'époque précédente (Xe siècle av. J.-C.). On y découvre que les Chinois avaient développé des méthodes de calcul et de démonstration qui leur étaient propres : arithmétique, fractions, extraction des racines carrées et cubiques, mode de calcul de l'aire du cercle, volume de la pyramide et méthode du pivot de Gauss. Leur développement des algorithmes de calcul est remarquablement moderne. Mais on trouve aussi, sur des os de moutons et de bœufs, des gravures prouvant que dès 1300 avant J.-C., ils utilisaient un système décimal positionnel (numération chinoise). Ils sont aussi à l'origine d'abaques les aidant à calculer. Les mathématiques chinoises avant notre ère sont principalement tournées vers les calculs utilitaires. Elles se développent ensuite de manière propre entre le Ier et le VIIe siècle après J.-C. puis entre le Xe et le XIIIe siècle.
Civilisations précolombiennes
La civilisation maya s'étend de 2600 avant J.-C. jusqu'à 1500 ans après J.-C. avec un apogée à l'époque classique du IIIe siècle au IXe siècle. Les mathématiques sont principalement numériques et tournées vers le comput calendaire et l'astronomie. Les Mayas utilisent un système de numération positionnel de base vingt (numération maya). Les sources mayas sont issues principalement des codex (écrits autour du XIIIe siècle). Mais ceux-ci ont été en grande majorité détruits par l'Inquisition et il ne reste de nos jours que quatre codex (celui de Dresde, de Paris, de Madrid et Grolier) dont le dernier est peut-être un faux.
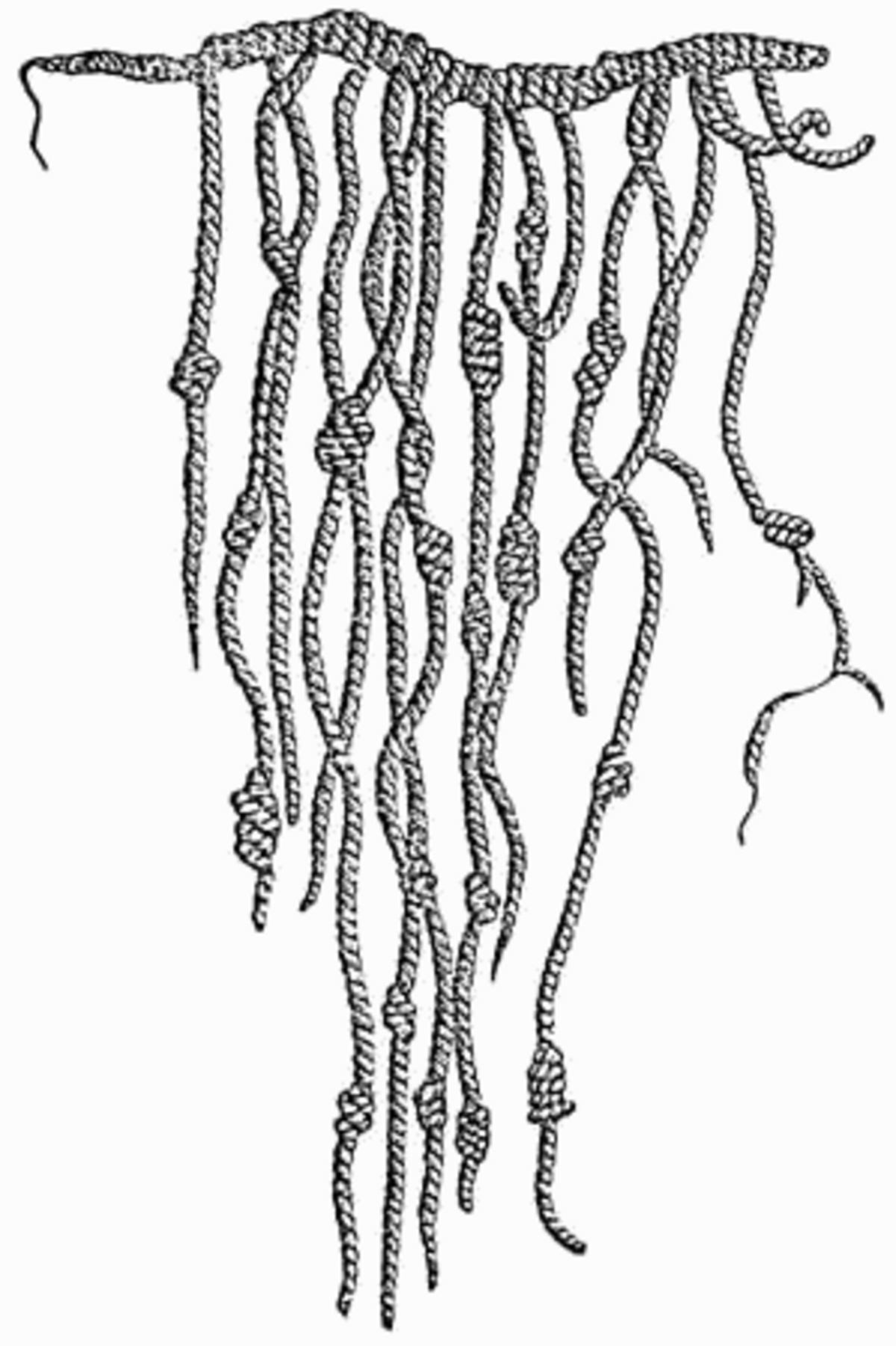
La civilisation Inca (1400-1530) a développé un système de numération positionnel en base 10 (donc similaire à celui utilisé aujourd'hui). Ne connaissant pas l'écriture[11], ils utilisaient des quipus pour " écrire " les statistiques de l'État. Un quipu est un encordage dont les cordes présentent trois types de nœuds symbolisant respectivement l'unité, la dizaine et la centaine[12]. Un agencement des nœuds sur une corde donne un nombre entre 1 et 999 ; les ajouts de cordes permettant de passer au millier, au million, etc.
Inde
La civilisation de la vallée de l'Indus développa un usage essentiellement pratique des mathématiques : système décimal de poids et mesures et régularité des proportions dans la confection de briques. Les sources écrites les plus anciennes concernant les mathématiques indiennes sont les sulba-sutras (de 800 av. J.-C. jusqu'à 200). Ce sont des textes religieux écrits en sanscrit réglementant la taille des autels de sacrifice. Les mathématiques qui y sont présentées sont essentiellement géométriques et sans démonstrations. On ignore s'il s'agit de la seule activité mathématique de cette époque ou seulement les traces d'une activité plus générale. Les Indiens connaissaient le théorème de Pythagore, savaient construire de manière exacte la quadrature d'un rectangle (construction d'un carré de même aire) et de manière approchée celle du cercle. On voit apparaître aussi des approximations fractionnaires de π et de racine carrée de deux. Vers la fin de cette période, on voit se mettre en place les neuf chiffres du système décimal.
Il faut ensuite attendre l'époque jaïniste (Ve siècle après J.-C.) pour voir naître de nouveaux textes mathématiques. Les mathématiciens de cette époque commencent une réflexion sur l'infini, développent des calculs sur des nombres de la forme 
qu'ils nomment première racine carrée, seconde racine carrée, troisième racine carrée. De cette époque, on peut citer l'Aryabhata (499) du nom de son auteur écrit en sanscrit et en vers et les traités d'astronomie et de mathématiques de Brahmagupta (598-670) . Dans le premier, on y trouve des calculs de volume et d'aire, des calculs de sinus qui donne la valeur de la demi-corde soutenue par un arc, la série des entiers, des carrés d'entiers, des cubes d'entiers. Une grande partie de ces mathématiques sont orientées vers l'astronomie. Mais on trouve aussi des calculs de dettes et recettes où l'on voit apparaître les premières règles d'addition et de soustraction sur les nombres négatifs. Mais c'est à Brahmagupta semble-t-il que l'on doit les règles opératoires sur le zéro en tant que nombre et la règle des signes.
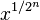
Grèce antique
Concernant les mathématiques grecques, aucun ouvrage original ne nous est parvenu. Il ne reste que des copies, des traductions et des commentaires via les mathématiques de langue arabe. On peut donc penser que ne nous sont parvenues que les œuvres majeures de cette époque.
La grande nouveauté des mathématiques grecques c'est qu'elles quittent le domaine de l'utilitaire pour rentrer dans celui de la pensée. Les mathématiques deviennent une branche de la philosophie. De l'argumentation philosophique découle l'argumentation mathématique. Il ne suffit plus d'appliquer, il faut prouver et convaincre : c'est la naissance de la démonstration. L'autre aspect de ces nouvelles mathématiques concerne leur objet d'étude. Au lieu de travailler sur des méthodes, les mathématiques étudient des objets, des représentations imparfaites d'objets parfaits, on ne travaille pas sur un cercle mais sur l'idée d'un cercle.
Les grandes figures de ces nouvelles mathématiques sont Thalès (-625 - -547), Pythagore (-580 - -490) et l'école pythagoricienne, Hippocrate (-470 - -410) et l'école de Chios, Eudoxe de Cnide (-408 - -355) et l'école de Cnide, Théétète d'Athènes (-415 - -369) puis Euclide.
De ses voyages en Égypte, Thalès rapporte en Grèce les connaissances en géométrie, travaille sur les triangles isocèles et les triangles inscrits dans un cercle.
De l'école pythagoricienne, nous pouvons retenir que tout est nombre. Les deux branches d'étude privilégiées sont l'arithmétique et la géométrie. La recherche d'objets parfaits conduit les Grecs à n'accepter d'abord comme nombres que les nombres rationnels matérialisés par la notion de longueurs commensurables : deux longueurs sont commensurables s'il existe une unité dans laquelle ces deux longueurs sont entières. L'échec de cette sélection matérialisée par l'irrationalité de la racine carrée de deux les conduit à n'accepter que les nombres constructibles à la règle et au compas. Ils se heurtent alors aux trois problèmes qui vont traverser l'histoire : la quadrature du cercle, la trisection de l'angle et la duplication du cube. En arithmétique, ils mettent en place la notion de nombre pair, impair, parfait et figuré. Leurs calculs sont d'autant plus remarquables que la numération grecque est certes décimale, mais additive. En géométrie, ils étudient les polygones réguliers avec une préférence pour le pentagone régulier.
Hippocrate de Chios cherchant à résoudre le problème mis en place par Pythagore découvre la quadrature des lunules et perfectionne le principe de la démonstration en introduisant la notion de problèmes équivalents.
Eudoxe de Cnide travaille sur la théorie des proportions acceptant ainsi de manipuler des rapports de nombres irrationnels. Il est probablement à l'origine de la formalisation de la méthode d'exhaustion pour le calcul par approximations successives d'aires et de volumes.
Théétète travaille sur les polyèdres réguliers.
Mais la révolution la plus importante vient des Éléments d'Euclide. Les objets géométriques doivent être définis : il ne s'agit plus d'objets imparfaits mais de l'idée parfaite des objets. Dans ses Éléments, Euclide se lance dans la première formalisation de la pensée mathématique. Il définit les objets géométriques (droites, cercles, angles), il définit l'espace par une série d'axiomes, il démontre par implication les propriétés qui en découlent et fait le lien formel entre nombre et longueur.
Après Euclide, deux grands noms éclairent les mathématiques grecques : Archimède qui perfectionne les méthode d'Eudoxe, et Apollonius dont le traité sur les coniques est considéré comme le sommet de la géométrie grecque.
Les mathématiques migrent alors à Alexandrie puis finissent pas se fondre dans les mathématiques de langue arabe.
Civilisations de langue arabe
Durant la période allant de 800 à 1500 après J.C., c'est dans les régions conquises par les musulmans que se développent les mathématiques. La langue arabe devient langue officielle des pays conquis. Un vaste effort de recueils et de commentaires de textes est entrepris. S'appuyant d'une part sur les mathématiques grecques, d'autre part sur les mathématiques indiennes et chinoises que leur relations commerciales leur permettent de connaître, les mathématiciens de langue arabe vont considérablement enrichir les mathématiques, développant l'embryon de ce qui deviendra l'algèbre, répandant le système décimal indien avec les chiffres improprement appelés chiffres arabes et développant des algorithmes de calculs. Parmi les nombreux mathématiciens de langue arabe, on peut citer Al-Khwarizmi et son ouvrage al-jabr. On assiste à un développement important de l'astronomie et de la trigonométrie.
Occident
Durant le Moyen Âge
Le rôle du Moyen Âge fut essentiel pour l'extension du domaine des nombres. C'est durant le Moyen Âge que l'application de l'algèbre au commerce amena en Orient l'usage courant des nombres irrationnels, un usage qui se transmettra ensuite à l'Europe. C'est aussi durant le Moyen Âge, mais en Europe, que pour la première fois des solutions négatives furent acceptées dans des problèmes. C'est enfin peu après la fin du Moyen Âge que l'on considéra les quantités complexes, qui permettaient de mettre en évidence des solutions réelles de certaines équations du troisième degré.
Durant la renaissance européenne
Dès le XIIe siècle est entreprise en Italie une traduction des textes arabes et, par la même, la redécouverte des textes grecs[13]. Tolède, ancien centre culturel de l'Espagne musulmane, devient, suite à la Reconquista, l'un des principaux centres de traduction, grâce au travail d'intellectuels comme Gérard de Crémone ou Adélard de Bath.
L'essor économique et commercial que connaît alors l'Europe, avec l'ouverture de nouvelles routes commerciales notamment vers l'Orient musulman, permet également aux milieux marchands de se familiariser avec les techniques héritées des arabes. Ainsi, Léonard de Pise, avec son Liber abaci en 1202, contribue largement à faire redécouvrir les mathématiques à l'Europe. Parallèlement au développement des sciences, se concentre une activité mathématique en Allemagne, en Italie et en Pologne aux XIVe siècle et XVe siècle. On assiste à un développement important de l'école italienne avec Cardan, Ferrari, Tartaglia, Scipione del Ferro, Bombelli, école principalement tournée vers la résolution des équations. Cette tendance est fortement liée au développement dans les villes italiennes de l'enseignement des mathématiques non plus dans un but purement théorique tel qu'il pouvait l'être dans le Quadrivium mais à des fins pratiques, notamment destinée aux marchands. Cet enseignement se diffuse dans des botteghe d'abbaco ou " écoles d'abbaques " ou des maestri enseigne l'arithmétique, la géométrie et les méthodes calculatoires à de futurs marchands à travers des problèmes récréatifs, connus grâce à plusieurs " traités d'abbaque " que ces maîtres nous ont laissé et étudiés que depuis peu par les historiens des sciences[14].
C'est suite aux travaux de Cardan et de Bombelli que les nombres complexes furent introduits. C'est le travail entrepris par Jérôme Cardan, Viète, Descartes qui développe fortement l'algèbre en Europe.
Jusqu'au XVIe siècle, la résolution de problèmes était principalement rhétorique. François Viète introduit le calcul symbolique avec des notations spécifiques pour les constantes et les variables.
Au XVIIe siècle
Les mathématiques portent leur regard sur des aspects physiques et techniques. Fils de deux pères, Isaac Newton et Gottfried Leibniz, le calcul infinitésimal fait entrer les mathématiques dans l'ère de l'analyse (dérivée, intégrale, équation différentielle).
Japon
Durant la période Edo (1603 - 1887), au Japon, se développe une mathématique sans influence de la mathématique occidentale mais inspirée de la mathématique chinoise, travaillant sur des problèmes d'essence géométrique. Des énigmes géométriques sont posées et résolues sur des tablettes en bois appelées Sangaku.
XIXe siècle
XXe siècle
Le métier de mathématicien a réellement commencé à se professionnaliser à la fin du XIXe siècle. Grâce à la globalisation, aux progrès des transports, la recherche mathématique n'est pas localisée sur un pays ou un continent. L'apparition de l'ordinateur a sensiblement modifié les conditions de travail des mathématiciens.
Le développement mathématique a explosé exponentiellement depuis 1900. De nouveaux domaines de recherche sont nés ou se sont développés : les systèmes dynamiques suite aux travaux de Poincaré, les probabilités, la topologie, la géométrie différentielle, la logique, la géométrie algébrique suite aux travaux de Grothendieck, ...
Notes et références
- ↑ Maurice Mashaal, p. 19
- ↑ La grande aventure de l'humanité, Arnold Toynbee, chap. 6
- ↑ Babylonian expedition voir ce document
- ↑ La tablette YBC 7289 prouve qu'ils connaissaient une valeur approchée de la racine carrée de deux au millionième près
- ↑ tablettes de Nippur
- ↑ Par exemple, la tablette de Plimpton 322
- ↑ http://www-history.mcs.st-andrews.ac.uk/HistTopics/Babylonian_mathematics.html
- ↑ Les mathématiques et l'astronomie babyloniennes dans Les sciences exactes dans l'Antiquité de O. NEUGEBAUER
- ↑ Maurice Mashaal, p. 23 et p. 26.
- ↑ Sylvia Couchoud, page ou chapitre à préciser
- ↑ Seules les données archéologiques apportent des informations sur leur organisation.
- ↑ Marcia Ascher, Mathématiques d'ailleurs, Nombres, Formes et Jeux dans les sociétés traditionnelles, Éditions du Seuil, 1998.
- ↑ Maurice Mashaal, p. 51.
- ↑ VAN EGMOND, Warren, The Commercial Revolution and the beginnings of Western Mathematics in Renaissance Florence, 1300-1500, éd. University of Michigan UMI Dissertation Services, Ann Arbor, Michigan, États-Unis, 628 p.