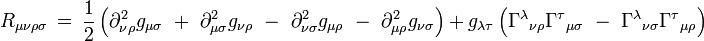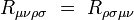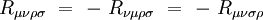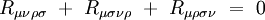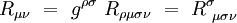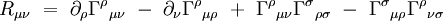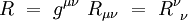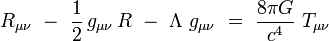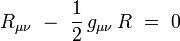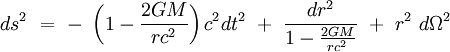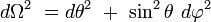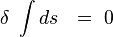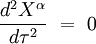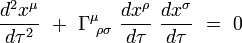Relativité générale - Définition
La relativité générale est une théorie relativiste de la gravitation. Dans ce cadre, la présence d'une masse déforme localement l’espace-temps. Le physicien Thibault Damour utilise à ce sujet l'expression imagée d'un espace-temps élastique.
Cette théorie est considérée comme l'œuvre majeure d’Albert Einstein, dont la construction l'occupa de 1907 à son achèvement, réalisé seulement à la fin de 1915. Aucun des nombreux tests expérimentaux effectués n'a pu la mettre en défaut à ce jour.
Généralités
Nécessité d'une théorie relativiste de la gravitation
La théorie de la gravitation proposée par Newton à la fin du XVIIe siècle[1] est basée sur la notion de force de gravitation agissant selon le principe d'action à distance. Ce caractère instantané est incompatible avec la théorie de la relativité restreinte proposée par Einstein en 1905. En effet, selon cette dernière, aucune information ne peut se propager plus vite que la vitesse de la lumière dans le vide. Par ailleurs, le principe de l'action à distance repose sur celui de la simultanéité de deux événements : la force que le Soleil exerce sur la Terre à un instant donné est déterminée par leurs propriétés " à cet instant ", indépendamment de la distance qui les sépare. La relativité restreinte stipule que le concept de simultanéité de deux événements n'est pas défini[2] : la proposition précédente est donc incompatible avec la relativité restreinte, censée être universelle. Cette contradiction amène Einstein à développer une théorie de la gravitation qui soit compatible avec la relativité restreinte. Le résultat de sa quête est la théorie de la relativité générale.
Géométries non euclidiennes
La description géométrique de la théorie physique due à Einstein trouve ses origines dans les avancées de la géométrie non euclidienne, qui résultent des différentes tentatives au cours des siècles de démontrer le cinquième postulat d’Euclide, qui énonce que : " par un point on ne peut mener qu’une parallèle à une droite donnée ". Ces efforts culminèrent au XIXe siècle avec la découverte par les mathématiciens Nicolaï Ivanovitch Lobatchevsky, János Bolyai et Carl Friedrich Gauss que ce postulat pouvait être remplacé par un autre (plusieurs parallèles possibles, ou pas de parallèle du tout), et ne constituait donc qu’un axiome arbitraire. Aucune de ces nouvelles géométries n’est plus " vraie " que celles d'Euclide : il s’agit simplement d’outils conceptuels différents pouvant servir de support à des usages également différents. La surface d’une sphère, par exemple, peut indifféremment être considérée comme la surface d’un objet dans un espace euclidien à 3 dimensions ou dans un espace non euclidien particulier à deux dimensions, la seconde représentation pouvant s’avérer plus commode dans certains cas.
Pour illustrer, si l’univers se caractérise par une telle géométrie, qu’un physicien tient un bâton verticalement, et qu’à une certaine distance, un cartographe mesure sa longueur par une technique de triangulation basée sur la géométrie euclidienne, rien ne garantit qu’il obtiendra le même résultat si le physicien lui apporte le bâton et qu’il le mesure directement.[3]
La généralisation de ces résultats, dénommée géométrie non euclidienne, fut réalisée par Bernhard Riemann, un élève de Gauss, mais elle fut considérée comme simple curiosité mathématique jusqu’à ce qu’Einstein utilise les travaux de son professeur Hermann Minkowski (qui utilisait des nombres complexes pour obtenir des espaces non euclidiens faciles à traiter en géométrie analytique… et exprima en 1907 dans cette description la transformation de Lorentz !) pour développer sa théorie de la relativité générale.
De la relativité de Galilée à la relativité restreinte
- Au XVIème siècle, Galilée affirme, et explique, que les lois de la physique sont les mêmes dans des référentiels en translation rectiligne et uniforme les uns par rapport aux autres. C'est le principe de relativité (de Galilée).
- Il utilisera aussi l'additivité des vitesses qui a comme conséquence que n'importe quelle vitesse peut être atteinte: ce n'est qu'une question de moyen. En un mot : si une balle roule à 10 km/h dans un train (et dans le sens de la marche) qui va lui-même à 100 km/h par rapport au sol, alors la balle va a 110 km/h par rapport au sol.
- Au XIXe siècle, le physicien écossais James Clerk Maxwell formula un ensemble d’équations, les équations du champ électromagnétique, qui conduisait à prédire la propagation d'ondes électromagnétiques de vitesse
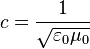
- Les théories corpusculaires de la lumière semblaient compatibles avec le principe de relativité de Galilée; ainsi que la théorie de Maxwell qui penchait en faveur de l'existence d'un Éther luminifère envisagé par Huygens. Mesurer la vitesse du système solaire par rapport à ce milieu élastique fut l'objet des expériences d’interférométrie menées par Michelson et Morley. Leurs expériences ont démontré que le vent apparent d'éther était nul, quelle que soit la période de l'année. Supposer que l'éther était constamment accroché à la terre aurait été une remise en cause trop grave du principe de relativité de Galilée. D'autre part, l'éther présentait l'inconvénient d'être à la fois impalpable et très "rigide" puisque capable de propager les ondes à une vitesse phénoménale.
- Il fallut attendre Einstein en 1905 pour remettre en cause radicalement la notion d'éther, porter au plus haut le principe de relativité de Galilée en postulant que les équations de Maxwell obéissent elles-mêmes à ce principe, et en tirer les conséquences révolutionnaires dans un article resté célèbre : De l’électrodynamique des corps en mouvement.
C'est la naissance de la relativité restreinte :
- Le principe de relativité de Galilée est conservé.
- L'invariance des équations de Maxwell entraîne immédiatement la constance de la vitesse de la lumière c dans tous les référentiels galiléens : l'additivité des vitesses n'est plus vraie et la vitesse de la lumière est inatteignable (sauf pour la lumière).
- Les mesures de longueur, d'intervalle de temps, (et de vitesse) ne sont pas les mêmes suivant le référentiel de l'observateur : mesurer la longueur du wagon donne des résultats différents suivant que l'on est dedans ou que l'on est immobile au sol (mais ce n'est pas le cas pour la largeur du wagon, longueur perpendiculaire à la vitesse); de même pour l'écoulement du temps; le champ électrique devient magnétique et réciproquement.. Toutes ces transformations des systèmes de coordonnées du continuum espace-temps et du champ électromagnétique sont formalisées par les transformations de Lorentz (paradoxalement mises au point par Lorentz et Henri Poincaré pour défendre l'existence de l'éther).
- La notion de temps absolu disparait: deux groupes de deux horloges parfaitement synchronisées immobiles dans un référentiel galiléen, et de deux horloges parfaitement synchronisées immobiles dans un autre référentiel galiléen présentent des défauts de synchronisation l'un par rapport à l'autre.
- En écrivant l'expression de l'énergie cinétique d'un corps de masse m de la manière la plus simple respectant le principe de relativité, Einstein a fait apparaître une énergie de repos E = mc2 dont le sens n'éclatera qu'une trentaine d'années plus tard lorsque Lise Meitner aura compris l'origine de l'énergie de fission nucléaire.
De la relativité restreinte à la Relativité Générale
La théorie de la relativité restreinte (1905) modifiait les équations utilisées pour comparer les mesures de longueur et de durée faites dans différents référentiels en mouvement les uns par rapport aux autres : cela eut pour conséquence que la physique ne pouvait plus traiter le temps et l’espace séparément, mais seulement comme un espace à quatre dimensions, l'espace-temps de Minkowski.
En effet, lors de mouvements à des vitesses non négligeables devant c (vitesse de la lumière dans le vide), temps et espace s’altèrent de façon liée, un peu comme deux coordonnées d’un point en géométrie analytique s’altèrent de façon liée lorsqu’on pivote les axes du repère.
Par exemple, en géométrie euclidienne habituelle la distance Δl entre deux points de coordonnées (x,y,z) et (x',y',z') vérifie (Δl)²= (Δx)²+(Δy)²+(Δz)² (avec Δx=x'-x, etc...), mais dans l'espace de Minkowski deux points sont repérés par les coordonnées (t,x,y,z) et (t',x',y',z'), où t et t' sont les coordonnées de temps, et la "distance" Δl entre ces points vérifie (Δl)²= (c.Δt)²-(Δx)²-(Δy)²-(Δz)². Ce calcul donne une "distance" nulle entre deux points du parcours d'un rayon lumineux, il donne aussi toutes les mesures de longueurs matérielles, des intervalles de temps, des vitesses en relativité restreinte qui succitent toujours l'étonnement.
L'espace-temps de Minkowski étant néanmoins de courbure nulle (c'est-à-dire plat) on le qualifie d'espace pseudo euclidien[4].
Tel devait être, pour Einstein, l'espace sans gravitation (et sans accélération pour l'observateur). La gravitation Newtonienne, se propageant instantanément, n'était pas compatible avec. Einstein se mit en quête d'une nouvelle théorie de la gravitation.
- Einstein admit l'égalité entre la masse gravifique et la masse inertielle comme hypothèse, la fameuse formule E=mc² autorisant alors à utiliser l'énergie totale d'un corps en lieu et place de sa masse. Ce sera fait grâce à l'outil mathématique nommé tenseur énergie.
- Expert en expériences par la pensée, il imagina un disque en rotation regardé par un expérimentateur placé en son centre et tournant avec: comme pour Huygens, il y a une force centrifuge au niveau du périmètre qui est perçue comme une force gravitationnelle (car la masse gravifique et la masse inerte sont égales par hypothèse). De plus, en voulant rester dans le cadre de la relativité restreinte, il conclue que l'observateur doit constater la réduction du périmètre mais pas du rayon: ce n'est pas possible dans un espace plat. Conclusion: la gravitation oblige à utiliser une géométrie non-euclidienne.
- Einstein imagina un expérimentateur enfermé dans un ascenseur aux parois opaques, subissant une montée à accélération constante : impossible pour cette personne de savoir s'il y a accélération constante ou bien attraction gravitationnelle (car la masse gravifique et la masse inerte sont égales par hypothèse). Conclusion: équivalence locale entre mouvement accéléré et gravitation, ce qui devait se retrouver dans les équations différentielles de la nouvelle théorie. C'est son principe d'équivalence.
- Enfin, Einstein voulait trouver une expression des lois de la nature (à l'époque: dynamique, gravitation et électromagnétisme) qui soit inchangée quel que soit le référentiel (accéléré ou galiléen, etc...): c'est la relativité galiléenne généralisée à tous les repères (on nomme cela la covariance).
- La grande difficulté étant de mettre ces principes sous forme mathématique, il en discuta avec David Hilbert qui, d'abord dubitatif, faillit lui ravir la vedette en trouvant la théorie en même temps que lui (voir: Controverse sur la paternité de la relativité).
La relativité générale ajouta à la relativité restreinte que la présence de matière pouvait déformer localement l’espace-temps lui-même (et non pas juste les trajectoires), de telle manière que des trajectoires dites géodésiques - c'est-à-dire intuitivement de longueur minimale - à travers l’espace-temps ont des propriétés de courbure dans l’espace et le temps.
Le calcul de la "distance" dans cet espace-temps courbé est plus compliqué qu'en relativité restreinte, en fait la formule de la "distance" est créée par la formule de la courbure, et vice-versa.
Les géodésiques sont les trajectoires, vérifiant le principe de moindre action, suivies par les particules test (c'est-à-dire dont l'influence sur le champ de gravitation dans lequel elles se déplacent est négligeable, ce qui est le cas par exemple d'un satellite artificiel autour de la Terre ou bien d'un photon passant à côté du Soleil mais pas d'une étoile orbitant autour d'une autre dans un système binaire oscillant rapidement), elles ont donc une importance pratique très importante pour la compréhension intuitive d'un espace courbe.
Conséquences théoriques et observations
- Einstein calcula immédiatement (1915) la déviation des positions apparentes des étoiles par le soleil: le 29 mai 1919, les mesures furent faites par Sir Arthur Eddington lors d’une éclipse solaire, et malgré quelques imprécisions de mesure, cela constitua la première confirmation de la théorie.
- Cette théorie prévoit une déviation lente de l'ellipse de révolution de Mercure qui concorde parfaitement avec les observations.
- La gravitation (forte) d'une planète doit y contracter les longueurs observées depuis une position lointaine. Cela n'a pu être observé directement à ce jour.
- La gravitation doit ralentir le temps, donc modifier les fréquences et les longueurs d'onde des rayonnements émis: on peut citer par exemple une expérience menée par Pound et Rebka à l'université Harvard (1959), qui a permis de détecter un changement de 22,5 mètres de la longueur d'onde d’une source monochromatique de Cobalt.
- Schwarzschild, en trouvant en 1916 une solution exacte des équations de la gravitation, a montré qu'il pouvait exister des conditions où un phénomène de trou noir apparaissait. L'astronomie observe des phénomènes similaires.
- Dans certaines conditions, des ondes gravitationnelles, discrètes, doivent se propager dans l'espace. L'expérience franco-italienne Virgo cherche à en détecter.
- Autre conséquence pratique de la relativité générale : les horloges atomiques en orbite autour de la Terre du système de positionnement GPS (Global Positioning System) nécessitent une correction pour le ralentissement dû à la gravité terrestre.
Pour plus de détails: tests expérimentaux de la relativité générale.
- Pour résumer cette théorie, Einstein amusa un public de journalistes : "Imaginez que vous regardez loin, très loin devant vous, et que vous avez une très bonne vue, une très très bonne vue, alors vous arriverez à voir... votre dos."
Résumé de la théorie
Référentiels
L’idée centrale de la relativité est que l’on ne peut pas parler de quantités telles que la vitesse ou l’accélération sans avoir auparavant choisi un cadre de référence, un référentiel, défini en un point donné. Tout mouvement est alors décrit relativement à ce référentiel. La relativité restreinte postule que ce référentiel peut être étendu indéfiniment dans l’espace et dans le temps. Elle ne traite que le cas des référentiels dits inertiels, autrement dits animés d’une vitesse constante et sans changement de direction. La relativité générale, elle, traite les référentiels accélérés (au sens vectoriel) ou non. En relativité générale, il est admis que l’on ne peut définir un référentiel local avec une précision donnée que sur une période finie et dans une région finie de l’espace (de la même manière, à cause de la courbure de la surface terrestre, on ne peut dessiner une carte sans distorsion que sur une région limitée). En relativité générale, les lois de Newton ne sont que des approximations valables dans un référentiel local inertiel. En particulier, la trajectoire de particules libres comme des photons est une ligne droite dans un référentiel local inertiel. Dès que ces lignes sont étendues au-delà de ce référentiel local, elles n’apparaissent plus droites, mais sont connues sous le nom de géodésiques. La première loi de Newton doit être remplacée par la loi du mouvement géodésique.
La trajectoire d’un photon est par exemple une géodésique de longueur… nulle : la partie positive du carré de cette longueur (x²+y²+z²) est en effet égale et opposée à sa partie négative (-c²t²)
Revenons sur la notion de référentiel inertiel. Nous distinguons les référentiels inertiels, dans lesquels un corps libre de toute action extérieure maintient un mouvement uniforme, des référentiels non inertiels, dans lesquels un corps libre subit une accélération dont l’origine est due à l’accélération du référentiel lui-même. Un exemple en est la force centrifuge que l’on ressent lorsqu’un véhicule qui nous transporte effectue un rapide changement de direction, un autre exemple en est la force dite de Coriolis, manifestation de la rotation terrestre. La force centrifuge est fictive et n'est qu'une manifestation de l'inertie (premier principe de Newton).
Principe d’équivalence
Parce qu’il n’a jamais été possible de mettre en évidence le moindre écart entre la masse d’inertie (résistance d’un corps à l’accélération) et la masse pesante (qui détermine son poids dans un champ de gravité), le principe d'équivalence en relativité générale postule qu’il n’y a pas lieu de distinguer localement un mouvement de chute libre (sans rotation) dans un champ gravitationnel, d’un mouvement uniformément accéléré en l’absence de champ gravitationnel. En clair, on n’observe pas localement de gravitation dans un référentiel en chute libre, en autant qu'il soit suffisamment petit, par rapport aux moyens de détection, pour qu'on ne puisse pas y détecter d'accélération. Autour de la Terre, la chute libre peut être par exemple une chute vers le sol ou bien le mouvement d’un satellite.
Ce résultat n’est que local, c’est-à-dire valable pour un espace restreint i.e. 'petit'. Dans un volume et avec des accéléromètres sensibles, on distinguera au contraire très bien un champ de gravité (forces concourantes), une simple accélération (forces parallèles) et un effet centrifuge (forces divergentes). Il s’agit juste d’unifier ce qui est semblable dans les phénomènes afin de les traiter par un mécanisme unique.
Cette équivalence est utilisée dans l’entraînement des astronautes : ceux-ci montent dans des avions effectuant un vol parabolique où la force centrifuge contrebalance quelques minutes les forces de gravité, simulant ainsi la " chute libre " d’un corps satellisé (chute libre qui dure indéfiniment, puisque circulaire).
Dans cette perspective, la gravitation observée à la surface terrestre est la force observée dans un référentiel défini en un point de la surface terrestre qui n’est pas libre, mais sur lequel agit toute la roche qui constitue le noyau, et cette force est de nature identique à la force centrifuge qui serait ressentie dans un vaisseau spatial suffisamment éloigné de la Terre pour ne plus guère subir son attraction, et effectuant une manœuvre de changement de direction. Ou encore, le sol empêche un objet de faire sa chute libre en exerçant une force vers le haut (appelée " réaction du sol ") ; en mécanique newtonienne, on a plutôt tendance à considérer que la chute libre est une accélération vers le bas, alors qu’ici, la chute libre est l’état de référence et c’est l’état de repos par rapport au sol qui est une accélération vers le haut.
Le principe d’équivalence revient à considérer, pour résumer, que la masse inertielle et la masse gravitationnelle représentent deux choses distinctes mais qui ont exactement la même valeur.
Tenseur d’énergie et courbure de l’espace
Mathématiquement parlant, Einstein modélise l’espace-temps par une variété pseudo-riemannienne quadri-dimensionnelle, et son équation du champ gravitationnel relie la courbure de la variété en un point, au tenseur impulsion-énergie en ce point, ce tenseur étant une mesure de la densité de matière et d’énergie (étant entendu que matière et énergie sont équivalentes).
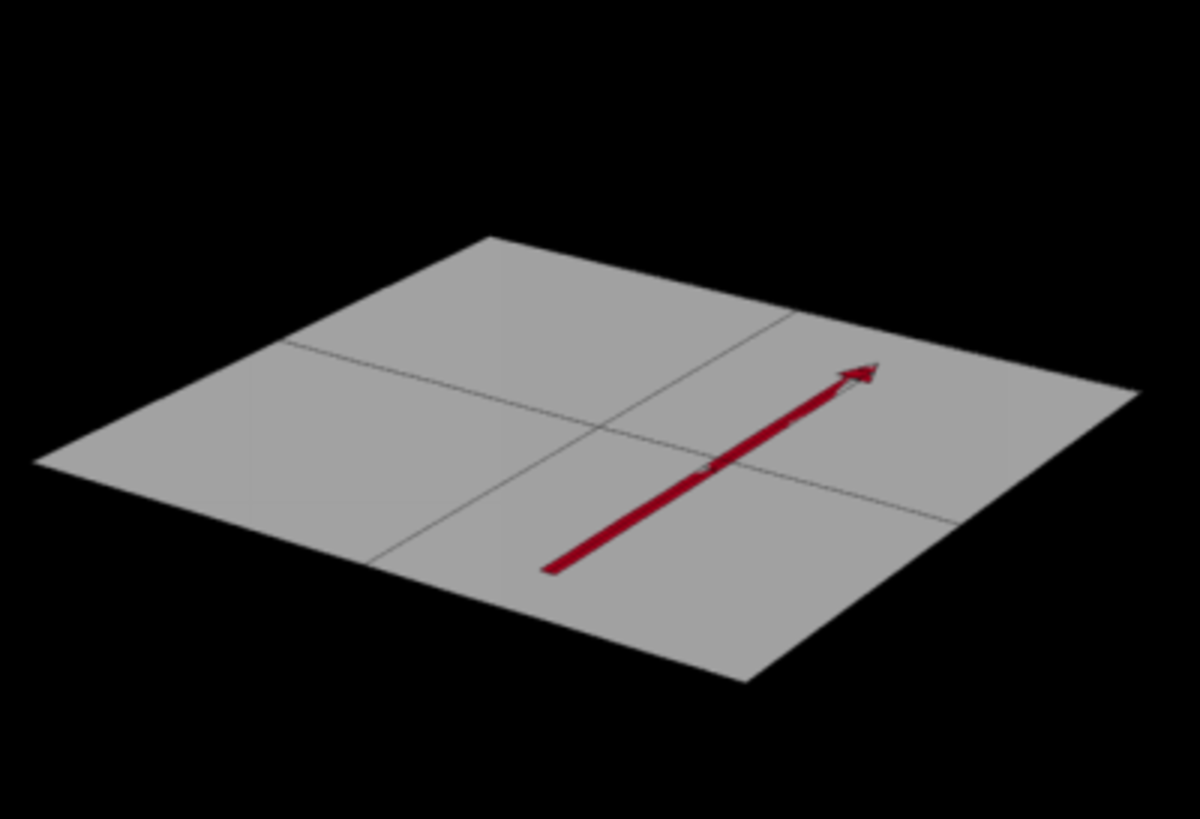
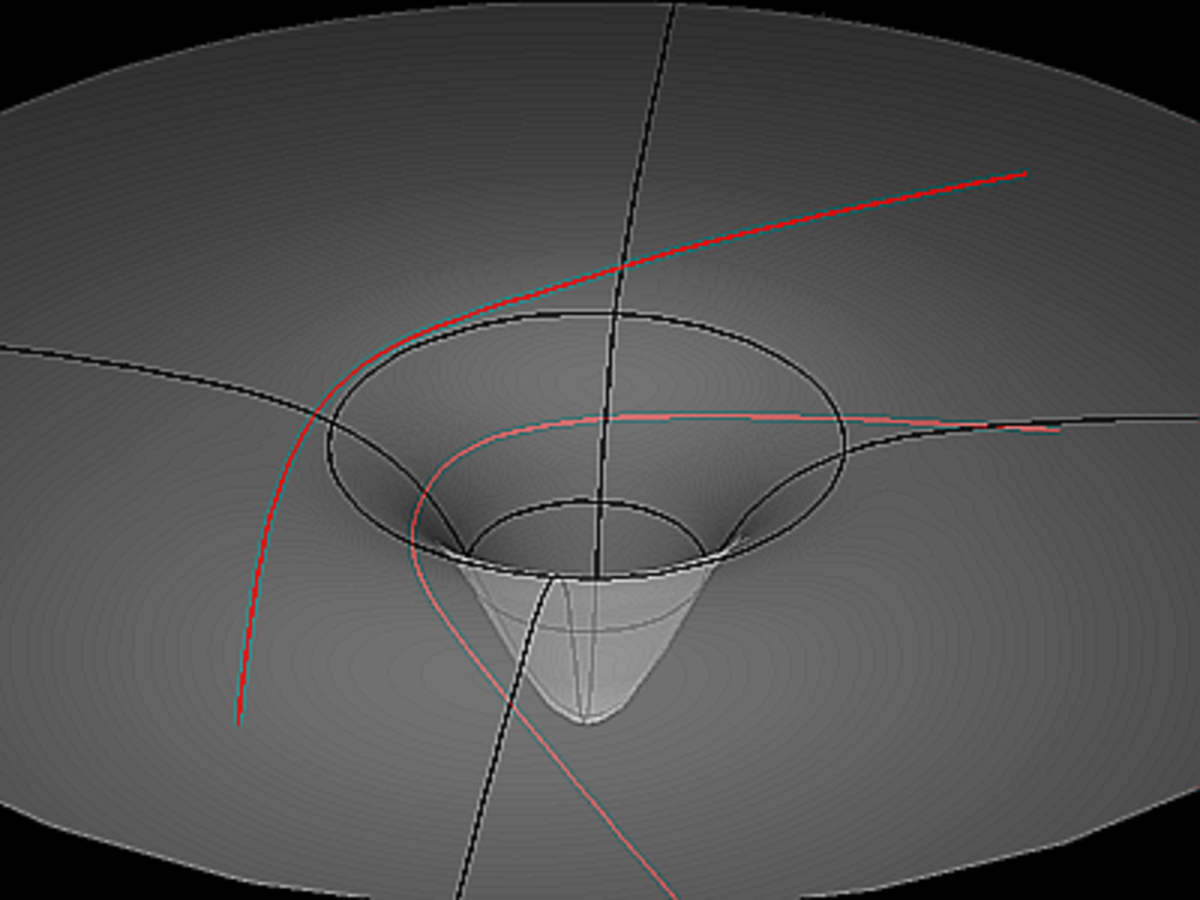
Cette équation est à la base de la fameuse formule qui dit que la courbure de l’espace définit le mouvement de la matière, et la matière définit la courbure de l’espace (les deux étant équivalents). La meilleure façon de se représenter la géométrie de l’espace-temps est d’imaginer que celui-ci se comporte comme une surface élastique creusée localement par la présence d’un objet massif, une boule par exemple.
Le chemin le plus court entre deux points - ce qui reste la définition de la " ligne droite " - ne sera alors pas le même qu’en l’absence de déformation : si la trajectoire passe trop près de la bille, en effet, le parcours est " allongé " par le creusement de la feuille de caoutchouc. Remarquons que nous n’avons à prendre en compte dans cette analogie ni le temps ni la gravité, ce qui est normal puisque c’est eux que nous désirons décrire en sortie.
En transposant cette image dans l’espace physique, la présence d’un corps massif affectera la courbure de l’espace, ce qui semblera vu de l’extérieur altérer la course d’un rayon lumineux ou d’un objet en mouvement qui passe dans son voisinage. Pour reprendre une expression célèbre due à John Archibald Wheeler : " La masse et l’énergie disent à l’espace-temps comment se courber, et la courbure de l’espace-temps dit à la matière comment se comporter ".
Cela a pour conséquence en astronomie l’effet de mirage gravitationnel (parfois nommé lentille gravitationnelle à tort, car n’ayant les propriétés ni d’une lentille convergente - ce que l’on voit immédiatement si l’on trace plus de quatre rayons ! - ni celles d’une lentille divergente).
Cette notion de courbure de l’espace explique la courbure des rayons lumineux au voisinage d’un astre massif, qui ne pouvait être due à la loi de Newton si les photons n’ont pas de masse.
L’équation du champ d’Einstein n’est pas une solution unique et il y a de la place pour d’autres modèles, s’ils sont en accord avec les observations.
La relativité générale se distingue des autres théories existantes par la simplicité du couplage entre matière et courbure géométrique, mais il reste à réaliser l’unification entre la relativité générale et la mécanique quantique, et le remplacement de l’équation du champ gravitationnel par une loi quantique plus générale.
Peu de physiciens doutent qu’une telle Théorie de Tout donnerait lieu aux équations de la relativité générale dans certaines limites d’application, de la même manière que cette dernière permet de prédire les lois de la gravitation de Newton dans les limites des faibles vitesses (dites vitesses non relativistes).
L’équation du champ contient un paramètre " supplémentaire " appelé la constante cosmologique Λ qui a été introduite à l’origine par Einstein pour qu’un univers statique (c’est-à-dire un univers qui n’est ni en expansion, ni en contraction) soit solution de son équation.
Cet effort se solda par un échec pour deux raisons : l’univers statique décrit par cette théorie était instable, et les observations de l’astronome Edwin Hubble dix ans plus tard démontrèrent que l’Univers était en fait en expansion. Donc Λ fut abandonnée, mais récemment, des techniques astronomiques ont montré qu’une valeur non nulle de Λ est nécessaire pour expliquer certaines observations.
L’étude des solutions de l'équation d'Einstein (Cf. paragraphe suivant) est une branche de la Physique nommée cosmologie. Elle permet notamment d’expliquer l’excès de l’avance du périhélie de Mercure, de prédire l’existence des trous noirs, des ondes gravitationnelles et d’étudier les différents scénarios d’évolution de l’Univers. Notons que l’astrophysicien bien connu Stephen Hawking a démontré qu’un univers comme le nôtre comportait nécessairement des singularités gravitationnelles.
Plus récemment (octobre 2004), des mesures effectuées par laser avec les satellites LAGEOS ont montré que le champ gravitationnel de la Terre lui-même engendre des distorsions de positionnement de la Lune de deux mètres par an comparativement à ce qui serait prévu par les seules lois de Newton. Ce chiffre est en accord à 1% près avec ce qui est prévu par la Relativité générale.
Aspects mathématiques
Nécessité d'une théorie relativiste de la gravitation
Mathématiquement, la force de gravitation de Newton dérive d'une énergie potentielle. Le potentiel de gravitation associé à cette énergie potentielle obéit à l'équation de Poisson, qui n'est pas covariante sous transformation de Lorentz. La théorie de la gravitation de Newton n'est donc pas compatible avec le principe fondamental de relativité restreinte énoncé par Einstein en 1905.
Ce principe étant supposé avoir une validité universelle, Einstein va chercher une théorie de la gravitation qui soit compatible avec lui. Le résultat de sa quête est la théorie de la relativité générale.
Modélisation de l'espace-temps
Notre perception intuitive nous indique que l'espace-temps apparait régulier et continu, c'est-à-dire " sans trous ". Mathématiquement, ces propriétés vont se traduire par le fait que l'espace-temps sera modélisé par une variété différentielle lisse[5] à 4 dimensions M4, c'est-à-dire un espace à 4 dimensions pour lequel le voisinage de chaque point ressemble localement à un espace euclidien à 4 dimensions.
Géométrie de l'espace-temps
NB Cet article suit les conventions de signe classiques de MTW [6]
Cet article adopte également la convention de sommation d'Einstein.
Tenseur métrique
La variété différentielle[7] M est munie d'une métrique lorentzienne définie par un tenseur métrique g, et constitue ainsi une variété lorentzienne, qui constitue un cas particulier de variété pseudo-riemannienne (le qualificatif " lorentzienne " sera précisé plus loin dans le texte ; cf. métrique lorentzienne).
Soit un système de coordonnées quelconque xμ autour d'un point P, et soient
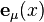
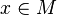
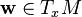
|
|
Les wμ sont appelée les composantes contravariantes du vecteur w. Le tenseur métrique
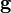
|
|
où dxμ désigne la base duale de
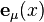
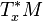
|
|
Les composantes gμν(x) du tenseur métrique varient de manière continue dans l'espace-temps[8].
Le tenseur métrique peut ainsi être représenté par une matrice 4x4 réelle symétrique :
|
|
Or, toute matrice 4x4 réelle possède a priori 4 x 4 = 16 éléments indépendants. La condition de symétrie réduit ce nombre à 10 : il reste en effet les 4 éléments diagonaux, auxquels il faut ajouter (16 - 4)/2 = 6 éléments non diagonaux. Le tenseur gμν possède donc seulement 10 composantes indépendantes.
Produit scalaire
Le tenseur métrique définit pour chaque point
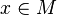
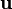
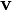
|
|
En particulier, en prenant deux vecteurs de base, on obtient les composantes :
|
|
Remarque : wμ désignant les composantes contravariantes du vecteur w, on peut définir de même ses composantes covariantes par :
|
|
Distance élémentaire
Considérons le vecteur déplacement élémentaire
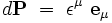
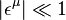
|
|
Si l'on note " à la physicienne " εμ = dxμ les composantes du vecteur déplacement élémentaire, la longueur infinitésimale s'écrit formellement :
|
|
Attention : dans cette formule, dxμ représente un nombre réel qui s'interprète physiquement comme la " variation infinitésimale " de la coordonnée xμ, et non une forme différentielle !
Métrique lorentzienne
Précisons maintenant l'expression lorentzienne, qui signifie que le tenseur métrique est de signature (1,3). Le principe d'équivalence assure qu'on peut effacer localement un champ de gravitation en prenant un système de coordonnées localement inertiel bien choisi. Dans un tel système de coordonnées localement inertiel Xα autour du point P précédent, l'invariant ds2 s'écrit :
|
|
où ηαβ est la métrique plate de Minkowski. On adopte ici la convention de signe MTW [6] :
|
|
On utilisera ici les conventions usuelles suivantes :
- un indice grec varie de 0 à 3. Il est associé à une grandeur dans l'espace-temps.
- un indice latin varie de 1 à 3. Il est associé aux composantes spatiales d'une grandeur dans l'espace-temps.
Par exemple, le 4-vecteur position s'écrit dans un système de coordonnées localement inertiel :
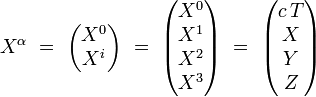
|
Le caractère lorentzien de la variété M assure ainsi que l'espace euclidien tangent à M possède en chaque point un pseudo-produit scalaire (pseudo au sens où l'hypothèse de positivité est retirée) ayant 3 valeurs propres strictement positives (associées à l'espace) et une valeur propre strictement négative (associée au temps). En particulier, l'intervalle élémentaire de temps propre séparant deux évènements vérifie :
|
|
Notions générales de connexion & dérivée covariante
D'une manière générale, on appelle connexion

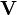
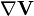
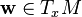
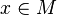
|
|
On dit que
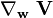
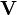
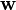
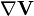
|
|
La dérivée covariante vérifie les deux propriétés de linéarité suivantes :
- linéarité en w, c'est-à-dire que, quelque soient les champs de vecteurs w et u et les nombres réels a et b, on ait :
|
|
- linéarité en V, c'est-à-dire que, quelque soient les champs de vecteurs X et Y et les nombres réels a et b, on ait :
|
|
Une fois que la dérivée covariante est définie pour les champs de vecteurs, elle peut être étendue aux champs tensoriels en utilisant la règle de Leibniz : si
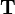
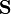
|
|
La dérivée covariante d'un champ de tenseur le long d'un vecteur w est à nouveau un champ de tenseur du même type.
Connexion associée à la métrique
On définit la connexion de Levi-Civita (lien) comme étant l'unique connexion vérifiant en plus des conditions précédentes que, pour tous champs de vecteurs X, Y, Z de TM, on ait :
-
-
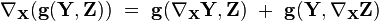
-
-
-
![\nabla_{\mathbf X} \mathbf Y \ - \ \nabla_{\mathbf Y} \mathbf X \ = \ [\mathbf X, \mathbf Y]](https://static.techno-science.net/illustration/Definitions/autres/4/41efd8f1632117de49de48bdea1cc393_b89dff58b086614725a17c49d4c62a17.png)
![[\mathbf X,\mathbf Y]](https://static.techno-science.net/illustration/Definitions/autres/6/6009e2fdb3c8442f213f534c97816c5d_346059339685d77b78069fcf380dc7d7.png)
-
Description en coordonnées
La dérivée covariante d'un vecteur est un vecteur, et peut ainsi être exprimée comme une combinaison linéaire de tous les vecteurs de base :
|
|
où Γρ représente la composante du vecteur dérivée covariante dans la direction
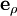
Pour décrire la dérivée covariante il suffit de décrire celle de chacun des vecteurs de base
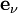
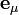
|
|
La connexion de Levi-Civita est entièrement caractérisée par ces symboles de Christoffel. Appliquons en effet la formule générale :
|
|
sous la forme :
|
|
Sachant que
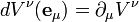
|
|
Le premier terme de cette formule décrit la "déformation" du système de coordonnées par rapport à la dérivée covariante, et le second les changements de coordonnées du vecteur V. Les indices sommés étant muets, on peut réécrire cette formule sous la forme :
|
|
On en déduit la formule importante pour les composantes :
|
|
En utilisant la formule de Leibniz, on démontrerait de même que :
|
|
Pour calculer explicitement ces composantes, les expressions des symboles de Christoffel doivent être déterminées à partir de la métrique. On les obtient aisément en écrivant les conditions suivantes :
|
|
Le calcul explicite de cette dérivée covariante conduit à :
|
|
où
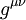
|
|
Les symboles de Christoffel ont une symétrie par rapport aux indices du bas :
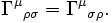
Remarque : on définit parfois aussi les symboles suivants :
|
|
tels que :
|
|
Tenseur de courbure de Riemann
Le tenseur de courbure de Riemann R est le tenseur d'ordre 4 défini pour tous champs de vecteurs X, Y, Z de M par :
|
|
Ses composantes s'écrivent explicitement en termes de la métrique :
|
|
Les symétries de ce tenseur sont :
|
|
|
|
Il vérifie de plus la relation :
|
|
Tenseur de courbure de Ricci
Le tenseur de Ricci est le tenseur d'ordre 2 défini par contraction du tenseur de courbure de Riemann :
|
|
Ses composantes s'écrivent explicitement en fonction de la métrique :
|
|
Ce tenseur est symétrique :
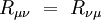
Courbure scalaire
La courbure scalaire est l'invariant défini par contraction du tenseur de Ricci avec la métrique :
|
|
Équation d'Einstein
L’équation complète du champ gravitationnel, qu'on appelle l'équation d'Einstein, s’écrit :
|
|
où Λ est la constante cosmologique, c est la vitesse de la lumière dans le vide, G est la constante gravitationnelle qui apparaît aussi dans la loi de la gravitation newtonienne, et Tμν le tenseur énergie-impulsion.
Le tenseur symétrique gμν possédant 10 composantes indépendantes, l'équation tensorielle d'Einstein est équivalente à un système de 10 équations scalaires indépendantes. Ce système aux dérivées partielles non linéaires couplées est le plus souvent très difficile à étudier.
Tenseur énergie-impulsion
Le tenseur énergie-impulsion peut s'écrire sous la forme d'une matrice 4x4 réelle symétrique :
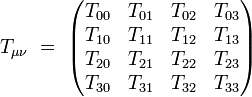
|
On y retrouve les grandeurs physiques suivantes :
- T00 est la densité volumique d'énergie. Elle est positive.
- T10, T20, T30 sont les densités de moments.
- T01, T02, T03 sont les flux d'énergie.
- La sous-matrice 3 x 3 des composantes spatiale-spatiale :
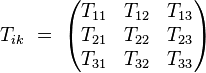
|
est la matrice des flux de moments. En mécanique des fluides, sa diagonale correspond à la pression, et les autres composantes correspondent aux efforts tangentiels dus à la viscosité.
Pour un fluide au repos, le tenseur énergie-impulsion se réduit à la matrice diagonale diag(ρc^2,p,p,p) où ρ est la masse volumique et p la pression hydrostatique.
Solutions particulières de l'équation d'Einstein
Dans le vide et pour une constante cosmologique identiquement nulle, l'équation d'Einstein se réduit à :
|
|
Dans le cas particulier d'un champ central engendré par un corps à symétrie sphérique, la métrique de Schwarzschild (16 janvier 1916) fournit une solution exacte à cette équation (qui n'est valide qu'à l'extérieur du corps) :
|
|
où M la masse totale du corps, et dΩ2 le carré de la distance élémentaire sur la sphère euclidienne de rayon unité en coordonnées sphériques :
|
|
- La métrique Friedmann-Lemaître-Robertson-Walker, où l'Univers est localement homogène et isotrope.
- L'espace de Sitter correspondant en physique à un Univers vide avec constante cosmologique positive.
- L'espace anti de Sitter correspondant en physique à un Univers vide avec constante cosmologique négative.
Problème à deux corps & problème du mouvement
En relativité générale, le problème à deux corps n'est pas exactement soluble ; seul le " problème à un corps " l'est. Cependant, on peut en général trouver une solution approchée pour ce qu'on appelle parfois le " problème du mouvement ".
Einstein & le problème du mouvement (1915)
Dans son manuscrit de la fin 1915, Einstein commence par calculer le champ de gravitation à symétrie sphérique crée par un astre de masse M lorsqu'on se place loin du centre de l'astre, le champ étant alors de faible intensité. Einstein explore ensuite le problème du mouvement d'une " particule test " de masse

Le principe d'équivalence avait par ailleurs conduit Einstein à postuler les équations du mouvement de la particule-test comme étant les équations dont les solutions sont certaines géodésiques de l'espace-temps. Mathématiquement, les géodésiques rendent la pseudo-distance extrêmale :
|
|
Dans un système de coordonnées localement inertielles Xα, ces équations du mouvement s'écrivent en composantes :
|
|
où τ est le temps propre de la particule test (supposée massive). Dans un système de coordonnées quelconques xμ, ces équations du mouvement prennent la forme suivante :
|
|
Les solutions de ces équations définissent les géodésiques du genre temps de l'espace-temps.
Einstein & le problème du mouvement (1938)
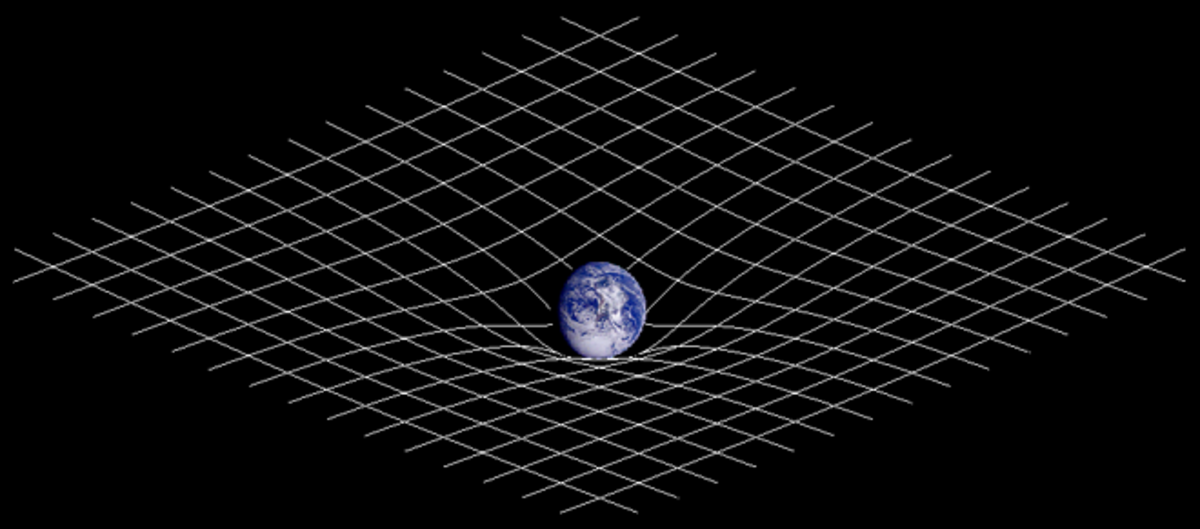
Dans son travail de 1938 réalisé en collaboration avec Infeld et Hoffmann, Einstein [10] va démontrer que les équations du mouvement de la particule-test :
|
|
dérivent des équations du champ. Il n'est donc pas nécessaire de les introduire par un postulat supplémentaire.
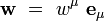
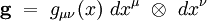
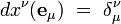
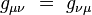
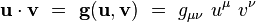
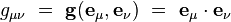
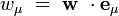
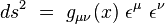
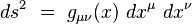
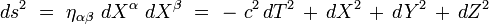
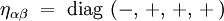
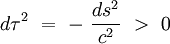
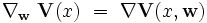
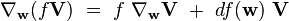
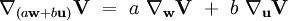
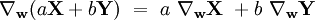
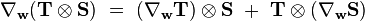
![\nabla_{\mathbf w} V \ = \ \left[ \, \nabla_{\mathbf w} V \, \right]^\rho \ \mathbf e_\rho \ = \ \Gamma^\rho \ \mathbf e_\rho](https://static.techno-science.net/illustration/Definitions/autres/2/2e6759695a5edb15bc6f7c5d3cc98eee_6c4a958992319d1b46390bdc501c9434.png)
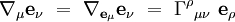
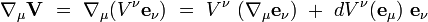
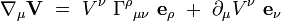
![\nabla_{\mu} \mathbf V \ = \ \left[ \, V^\rho \ \Gamma^\nu {}_{\mu \rho} \ + \ \partial_\mu V^\nu \, \right] \ \mathbf e_\nu](https://static.techno-science.net/illustration/Definitions/autres/a/ad0fab9404fb416af7949fff289ba8c1_583499bc8fb632766f874391a1befb21.png)
![\nabla_{\mu} \mathbf{V}^{\nu} \ = \ \left[ \, \nabla_{\mu} \mathbf{V} \, \right]^{\nu} \ = \ \partial_{\mu} V^{\nu} \ + \ \Gamma_{~ \mu \rho}^{\nu} \ V^{\rho}](https://static.techno-science.net/illustration/Definitions/autres/6/66801a9cd9441b2220dfd8cf98fc4fda_508795177294bfe43a2c0628c8018af1.png)
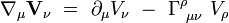
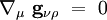
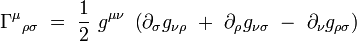
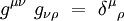
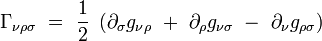
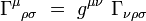
![\mathbf R(\mathbf X,\mathbf Y)\mathbf Z \ = \ \nabla_{\mathbf X} \, (\nabla_{\mathbf Y} \mathbf Z) \ - \ \nabla_{\mathbf Y} \, (\nabla_{\mathbf X} \mathbf Z) \ - \ \nabla_{[\mathbf X,\mathbf Y]} \mathbf Z](https://static.techno-science.net/illustration/Definitions/autres/9/9297569b2b761e145ea2c28a12fae9d6_f333f1ac3a3cbb0c3d47cd9e5e953694.png)